TorchOpt: An Efficient Library for Differentiable Optimization

An overview for our NeurIPS 2022 Workshop OPT paper, TorchOpt - An Efficient Library for Differentiable Optimization. In this paper, we introduce TorchOpt, a PyTorch-based efficient library for differentiable optimization. This library provides unified and expressive differentiable optimization programming abstraction, and high-performance distributed execution runtime.

Introduction

Differentiable programming has revolutionized the field of machine learning (ML) by enabling automatic computation of derivatives of functions within a high-level language. It has been widely used within backpropagation of neural networks, probabilistic programming, and Bayesian inference. This has empowered ML and its applications, allowing for efficient and composable automatic differentiation (AD) tools that have led to advances in optimization, differentiable simulators, engineering, and science. The recent boom in various differentiable optimization algorithms has further cemented the importance of differentiable programming. Differentiable optimization usually involves optimizing parameters by differentiating through an optimization process, which can be represent as follows

\[\boldsymbol{\theta}_0 \xrightarrow{\boldsymbol{\phi}} \boldsymbol{\theta}_1 \xrightarrow{\boldsymbol{\phi}} \boldsymbol{\theta}_2 \xrightarrow{\boldsymbol{\phi}} \cdots \boldsymbol{\theta}^{\prime}\]

where \(\boldsymbol{\theta}\) are inner-loop policy parameters, \(\boldsymbol{\phi}\) are meta parameters. The inner-loop optimization process is usually a black-box function that can be represented as a differentiable function.

These algorithms exhibit different execution patterns, and their execution needs massive computational resources that go beyond a single CPU and GPU. Existing differentiable optimization libraries, however, cannot support efficient algorithm development and multi-CPU/GPU execution, making the development of differentiable optimization algorithms often cumbersome and expensive. This blog introduces TorchOpt, a PyTorch-based efficient library for differentiable optimization. TorchOpt provides a unified and expressive differentiable optimization programming abstraction. This abstraction allows users to efficiently declare and analyze various differentiable optimization programs with explicit gradients, implicit gradients, and zero-order gradients. TorchOpt further provides a high-performance distributed execution runtime. This runtime can fully parallelize computation-intensive differentiation operations (e.g. tensor tree flattening) on CPUs / GPUs and automatically distribute computation to distributed devices.

---

Unified and expressive differentiation mode for differentiable optimization

TorchOpt's differentiation modes. By formulating the problem as a differentiable problem, TorchOpt offers Autograd support for the backward pass (dotted lines).

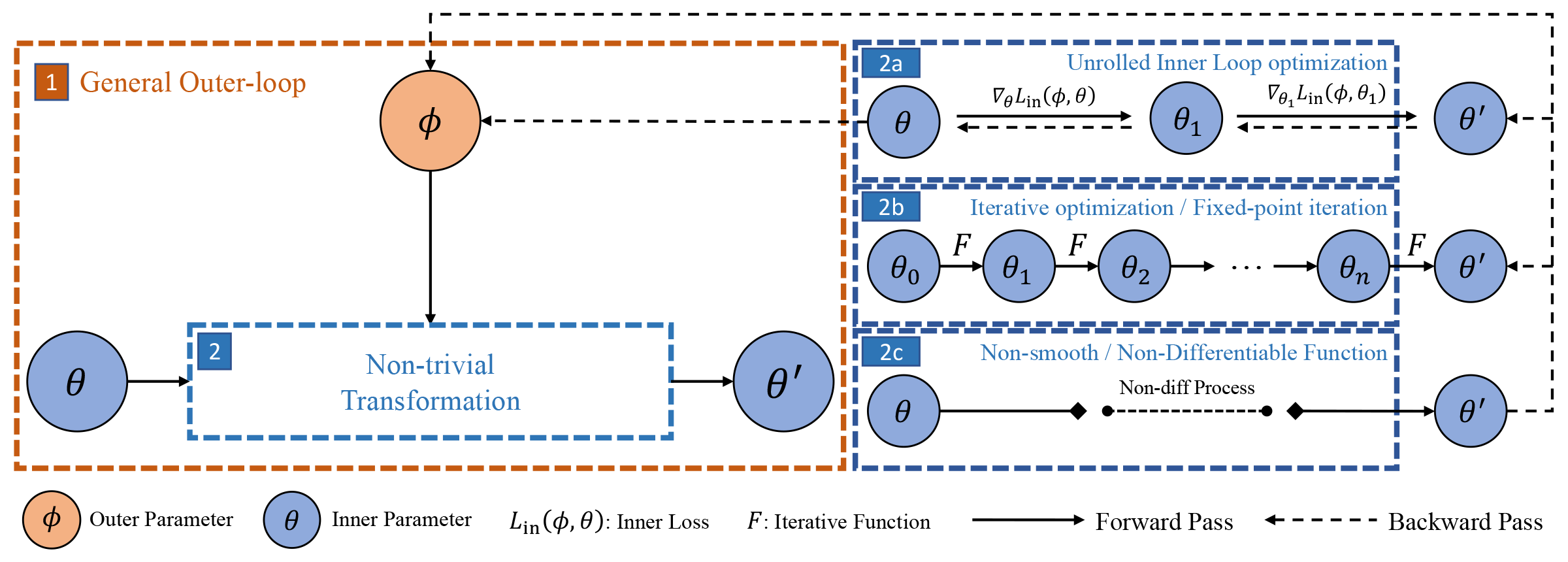
As shown in figure above, the scheme contains an outer level that has parameters \(\boldsymbol{\phi}\) that can be learned end-to-end through the inner level parameters solution \(\boldsymbol{\theta}^{\prime}(\boldsymbol{\phi})\) (treating solution $\boldsymbol{\theta}^{\prime}$ as a function of \(\boldsymbol{\phi}\)) by using the best-response derivatives \(\partial \boldsymbol{\theta}^{\prime}(\boldsymbol{\phi})/ \partial \boldsymbol{\phi}\). It can be seen that the key component of this algorithm is to calculate the best-response (BR) Jacobian. From the BR-based perspective, TorchOpt supports three differentiation modes: explicit gradient over unrolled optimization, implicit differentiation, and zero-order differentiation.

Explicit gradient differentiation

As shown in figure-2a above, the idea of explicit gradient differentiation is to treat the gradient step as a differentiable function and try to backpropagate through the unrolled optimization path. This differentiation mode is suitable for algorithms when the inner-level optimization solution is obtained by a few gradient steps, such as MAML and MGRL .

Implicit gradient differentiation

As shown in figure-2b above, by treating the solution \(\boldsymbol{\theta}^{\prime}\) as an implicit function of \(\boldsymbol{\phi}\), the idea of implicit gradient differentiation is to directly get analytical best-response derivatives \(\partial \boldsymbol{\theta}^{\prime}(\boldsymbol{\phi})/ \partial \boldsymbol{\phi}\) by implicit function theorem . This is suitable for algorithms when the inner-level optimal solution is achieved (\({\left. \frac{\partial F(\boldsymbol{\theta},\boldsymbol{\phi})}{\partial \boldsymbol{\theta}} \right\rvert}_{\boldsymbol{\theta}^{\prime}} = 0\)) or reaches some stationary conditions (\(F(\boldsymbol{\theta}^{\prime},\boldsymbol{\phi})=0\)), such as iMAML and DEQ . TorchOpt offers functional/OOP API for supporting both conjugate gradient-based and Neumann series-based method.

Zero-order gradient differentiation

As shown in figure-2c above, when the inner-loop process is non-differentiable or one wants to eliminate the heavy computation burdens in the previous two modes (brought by Hessian), one can choose zero-order gradient differentiation. Zero-order gradient differentiation typically gets gradients based on zero-order estimation, such as finite-difference, or Evolutionary Strategy (ES) . ESMAML , and NAC , successfully solve the differentiable optimization problem based on ES. Instead of optimizing the objective \(F\), ES optimizes a Gaussion smoothing objective defined as \(\tilde{f}_\sigma(\boldsymbol{\theta}) = \mathbb{E}_{\boldsymbol{z} \sim \mathcal{N}\left(\mathbf{0}, \boldsymbol{I}_d\right)} f (\boldsymbol{\theta} + \sigma \boldsymbol{z})\), where \(\sigma\) denotes precision. The gradient of such objective is \(\nabla_\theta \tilde{f}_\sigma(\theta) = \frac{1}{\sigma} \mathbb{E}_{\boldsymbol{z} \sim \mathcal{N}\left(\mathbf{0}, \boldsymbol{I}_d\right)} f(\boldsymbol{\theta} + \sigma \boldsymbol{z}) \boldsymbol{z}\).

---

High-performance and distributed execution runtime

CPU/GPU-accelerated optimizers

We take the optimizer as a whole instead of separating it into several basic operators (e.g., \(\texttt{sqrt}\) and \(\texttt{div}\)). Therefore, by manually writing the forward and backward functions, we can perform the symbolic reduction. In addition, we can store some intermediate data that can be reused during the back-propagation. Our design reduces computation and also benefits numerical stability (by explicitly canceling some \(0/0\) cases in higher gradient computation). We write the accelerated functions in C++ OpenMP and CUDA, bind them by \(\texttt{pybind11}\) to allow Python can call them, and then we define the forward and backward behavior using \(\texttt{torch.autograd.Function}\).

Memory-efficient and cache-friendly PyTree utilities

The tree operations (e.g., flatten and unflatten) are frequently called by the functional and Just-In-Time (JIT) components in TorchOpt. To enable memory-efficient nested structure flattening, we implement the pytree utilities, named \(\texttt{OpTree}\). By optimizing their memory and cache performance (e.g., \(\texttt{absl::InlinedVector}\)), TorchOpt can significantly improve the performance of differentiable optimization at scale.

Distributed differentiable optimization

TorchOpt allows users to reduce training time by using parallel GPUs. Different from existing MPI-based synchronous training and asynchronous model averaging systems, TorchOpt adopts RPC as a flexible yet performance communication backend. The distributed GPUs perform differentiable optimization tasks in parallel. These GPUs are coordinated by a chosen GPU device which realizes the synchronous execution of parallel GPUs, thus guaranteeing the convergence of the model in a distributed training setting. TorchOpt distributes a differentiable optimization job across multiple GPU workers and executes the workers in parallel. TorchOpt users can wrap code in the distributed Autograd module and achieve substantial speedup in training time with only a few changes in existing training scripts.

---

Applications

We offer several applications with TorchOpt. These applications are based on the following three differentiable optimization algorithms: iMAML , MGRL , and MAML on distributed device.

Implicit Model-Agnostic Meta-Learning (IMAML)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
 
import copy
from collections import OrderedDict
from types import FunctionType

import functorch
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.types
from torch.utils import data

import helpers
import torchopt
from torchopt import pytree

@torch.no_grad()
def get_model_torch(
    device: torch.types.Device = None, dtype: torch.dtype = torch.float32
) -> tuple[nn.Module, data.DataLoader]:
    helpers.seed_everything(seed=42)

    model = FcNet(MODEL_NUM_INPUTS, MODEL_NUM_CLASSES).to(dtype=dtype)

    if device is not None:
        model = model.to(device=torch.device(device))

    dataset = data.TensorDataset(
        torch.randint(0, 1, (BATCH_SIZE * NUM_UPDATES, MODEL_NUM_INPUTS)),
        torch.randint(0, MODEL_NUM_CLASSES, (BATCH_SIZE * NUM_UPDATES,)),
    )
    loader = data.DataLoader(dataset, BATCH_SIZE, shuffle=False)

    return model, loader


model, loader = get_model_torch(device='cpu')

fmodel, params = functorch.make_functional(model)
optim = torchopt.sgd(lr)
optim_state = optim.init(params)

def imaml_objective_torchopt(params, meta_params, data):
    x, y, f = data
    y_pred = f(params, x)
    regularization_loss = 0
    for p1, p2 in zip(params, meta_params):
        regularization_loss += 0.5 * torch.sum(torch.square(p1 - p2))
    loss = F.cross_entropy(y_pred, y) + regularization_loss
    return loss

@torchopt.diff.implicit.custom_root(
    functorch.grad(imaml_objective_torchopt, argnums=0),
    argnums=1,
    has_aux=True,
    solve=torchopt.linear_solve.solve_normal_cg(),
)
def inner_solver_torchopt(params, meta_params, data):
    # Initial functional optimizer based on TorchOpt
    x, y, f = data
    optimizer = torchopt.sgd(lr=inner_lr)
    opt_state = optimizer.init(params)
    with torch.enable_grad():
        # Temporarily enable gradient computation for conducting the optimization
        for _ in range(inner_update):
            pred = f(params, x)
            loss = F.cross_entropy(pred, y)  # compute loss
            # Compute regularization loss
            regularization_loss = 0
            for p1, p2 in zip(params, meta_params):
                regularization_loss += 0.5 * torch.sum(torch.square(p1 - p2))
            final_loss = loss + regularization_loss
            grads = torch.autograd.grad(final_loss, params)  # compute gradients
            updates, opt_state = optimizer.update(grads, opt_state, inplace=True)  # get updates
            params = torchopt.apply_updates(params, updates, inplace=True)
    return params, (0, {'a': 1, 'b': 2})

for xs, ys in loader:
    xs = xs.to(dtype=dtype)
    data = (xs, ys, fmodel)
    inner_params = pytree.tree_map(
        lambda t: t.clone().detach_().requires_grad_(requires_grad=t.requires_grad), params
    )
    optimal_inner_params, aux = inner_solver_torchopt(inner_params, params, data)
    assert aux == (0, {'a': 1, 'b': 2})
    outer_loss = fmodel(optimal_inner_params, xs).mean()

    grads = torch.autograd.grad(outer_loss, params)
    updates, optim_state = optim.update(grads, optim_state)
    params = torchopt.apply_updates(params, updates)

    xs = xs.numpy()
    ys = ys.numpy()
 

Meta-gradient reinforcement learning (MGRL)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
 
import torch
import torch.nn as nn
import torch.nn.functional as F

import torchopt


def test_gamma():
    class Rollout:
        @staticmethod
        def get():
            out = torch.empty(5, 2)
            out[:, 0] = torch.randn(5)
            out[:, 1] = 0.1 * torch.ones(5)
            label = torch.arange(0, 10)
            return out.view(10, 1), F.one_hot(label, 10)

        @staticmethod
        def rollout(trajectory, gamma):
            out = [trajectory[-1]]
            for i in reversed(range(9)):
                out.append(trajectory[i] + gamma[i] * out[-1].clone().detach_())
            out.reverse()
            return torch.hstack(out).view(10, 1)

    class ValueNetwork(nn.Module):
        def __init__(self):
            super().__init__()
            self.fc = nn.Linear(10, 1)

        def forward(self, x):
            return self.fc(x)

    torch.manual_seed(0)
    inner_iters = 1
    outer_iters = 10000
    net = ValueNetwork()
    inner_optimizer = torchopt.MetaSGD(net, lr=5e-1)
    gamma = torch.zeros(9, requires_grad=True)
    meta_optimizer = torchopt.SGD([gamma], lr=5e-1)
    net_state = torchopt.extract_state_dict(net)
    for i in range(outer_iters):
        for j in range(inner_iters):
            trajectory, state = Rollout.get()
            backup = Rollout.rollout(trajectory, torch.sigmoid(gamma))
            pred_value = net(state.float())

            loss = F.mse_loss(pred_value, backup)
            inner_optimizer.step(loss)

        trajectory, state = Rollout.get()
        pred_value = net(state.float())
        backup = Rollout.rollout(trajectory, torch.ones_like(gamma))

        loss = F.mse_loss(pred_value, backup)
        meta_optimizer.zero_grad()
        loss.backward()
        meta_optimizer.step()
        torchopt.recover_state_dict(net, net_state)
        if i % 100 == 0:
            with torch.no_grad():
                print(f'epoch {i} | gamma: {torch.sigmoid(gamma)}')


if __name__ == '__main__':
    test_gamma()
 

Distributed Model-Agnostic Meta-Learning (MAML)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
 
import torch
import torch.nn as nn
import torchopt.distributed as todist

def parse_arguments():
    parser = argparse.ArgumentParser(description='TorchOpt Distributed Training')
    ...

    args = parser.parse_args()
    return args

def worker_init_fn():
    # set process title, seeding, etc.
    setproctitle.setproctitle(f'Worker{todist.get_rank()}')
    torch.manual_seed(args.seed + todist.get_rank())

@todist.parallelize(partitioner=todist.batch_partitioner, reducer=todist.mean_reducer)
def compute_loss(model, batch):
    device = torch.device(f'cuda:{todist.get_local_rank()}')
    model = model.to(device)
    batch = batch.to(device)

    # Compute local loss of the given batch
    ...
    return loss.cpu()

def build_model():
    return nn.Sequential(
        ...
    )

@todist.rank_zero_only
def train(args):
    model = build_model()
    optimizer = torch.optim.SGD(model.parameters(), lr=args.lr)
    train_loader = ...

    for epoch in range(args.epochs):
        for batch in train_loader:
            with todist.autograd.context() as context_id:
                # Forward pass
                cloned_model = todist.module_clone(model, by='clone')
                loss = compute_loss(cloned_model, batch)

                # Backward pass
                optimizer.zero_grad()
                todist.autograd.backward(context_id, loss)

                # Update parameters
                optimizer.step()

@todist.auto_init_rpc(worker_init_fn)
def main():
    args = parse_arguments()
    train(args)

if __name__ == '__main__':
    main()
 

Conclusion

This blog introduces TorchOpt, a novel efficient differentiable optimization library for PyTorch. Experimental results show that TorchOpt can act as a user-friendly, high-performance, and scalable library when supporting challenging gradient computation with PyTorch. In the future, we aim to support more complex differentiation modes and cover more non-trivial gradient computation problems, such as adjoint methods for the gradient of ODE solutions, RL or Gumbel-Softmax method for differentiating through discrete distribution, and differentiable combinatorial solvers. TorchOpt has already been used for meta-gradient research problem and we believe it can be served as an important auto-differentiation tool for more differentiable optimization problems.